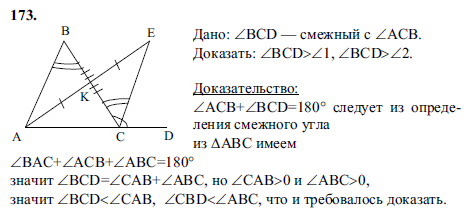
Докажите, что угол, смежный с углом треугольника, больше каждого из двух других углов треугольника

Решение. Пусть угол BAD — смежный с углом А треугольника ABC (рис.97). Докажем, например, что ZBAD > АВ.
Отметим середину О стороны АВ и на продолжении отрезка СО отложим отрезок ОЕ, равный СО. Тогда АВОС = = ААОЕ по двум сторонам и углу между ними. Отсюда следует, что АВ = = Z1. Но ZBAD > Z1 и, следовательно, ZBAD > ZB.