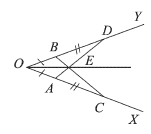
На сторонах угла XOY отмечены точки А, В, С и D так, что ОА=ОВ, AC=BD
Чтобы оставить ответ, войдите или зарегистрируйтесь.

Решение. AOAD = АОВС по двум сторонам и углу между ними (ОА = OB, OD = ОС, угол О — общий). Отсюда следует, что ZODA = ZOCB.
Сравним треугольники BDE и АСЕ. В этих треугольниках BD = = AC, ZBDE = ZACE и углы с вершиной Е равны как вертикальные. Поэтому ABDE = ААСЕ (см. задачу 174), и, следовательно, BE = АЕ.
АОАЕ = АОВЕ по трем сторонам. Отсюда следует, что ZAOE = ZBOE, т. е. луч ОЕ — биссектриса угла XOY.
Биссектрису данного угла с вершиной О можно построить следующим образом. На сторонах угла откладываем равные отрезки О А и ОВ, АС и BD, как показано на рисунке 99. Затем проводим отрезки AD и ВС. Они пересекаются в некоторой точке Е. Остается провести луч ОЕ — это и есть биссектриса данного угла.