Даны три точки А, B, С, лежащие на одной прямой, и точка D, не лежащая

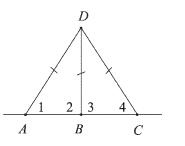
Решение. Пусть точка В лежит между А и С. Предположим, что AD = BD = = CD (рис. 102). Тогда треугольники ADB, BDC и ADC — равнобедренные, откуда следует, что Z1 = Z2, Z3 = Z4 и Zl = Z4,  т. е. углы 1, 2, 3 и 4 равны друг другу. Но углы 2 и 3 — смежные, поэтому Z2 + Z3 = 2Z2 = 180°, откуда Z2 = 90°. Итак, Zl = Z2 = = Z3 = Z4 = Z90°, т. е. из точки D проведены три перпендикуляра к прямой АС, чего не может быть. Следовательно, наше предположение о равенстве отрезков AD, BD и CD неверно. Поэтому хотя бы два из этих отрезков не равны друг другу.