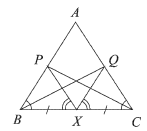
На боковых сторонах АВ и АС равнобедренного треугольника ABC отмечены точки Р и Q так,

Решение. Так как треугольник ABC — равнобедренный с основанием ВС, то ZB = = АС (рис. 103).
АВРХ = ACQX по стороне и двум прилежащим углам  (ВХ = СХ и ZPXB = ZQXC по условию, ZB = ZC).
Отсюда следует, что ВР = CQ АВРС = ACQB по двум сторонам и углу между ними (ВР = CQ, ВС — общая сторона,   ZB = ZC), поэтому СР = BQ, что и требовалось доказать.