Необходимо измерить на местности расстояния между точками А и В, из которых одна (точка А)

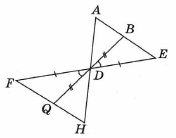
На местности провешивают направление отрезка АВ и на его продолжении отмеряют произвольный отрезок BE. Выбирают на местности точку D, из которой видна точка А и можно пройти к точкам В и Е. Провешивают прямые BDQ и EDF и отмеряют FD = DE и DQ = BD. Затем идут по прямой FQ, глядя на точку А, пока не найдут точку Н, которая лежит на пересечении прямых AD и FQ. Тогда искомое расстояние АВ будет равно длине отрезка QH. Докажем это.
Треугольники FDQ и EDB равны по двум сторонам и углу между ними. Углы FDQ и EDB равны как вертикальные, а соответствующие стороны равны по построению. Из равенства треугольников следует равенство углов EBD и FQD, а значит, и смежных с ними углов ABD и HQD. Углы ADB и HDQ равны как вертикальные. Следовательно, треугольники ABD и HQD равны по стороне и прилежащим к ней углам. Из равенства треугольников и следует, что HQ равно искомому расстоянию АВ.